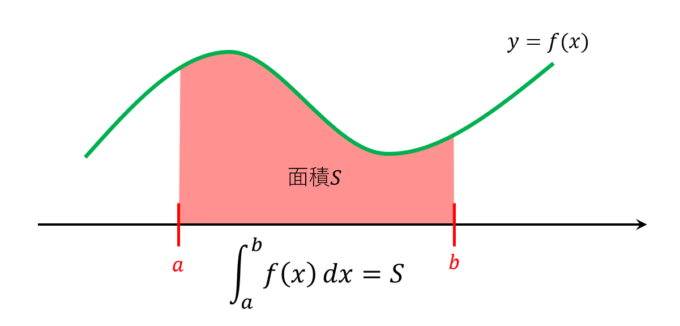
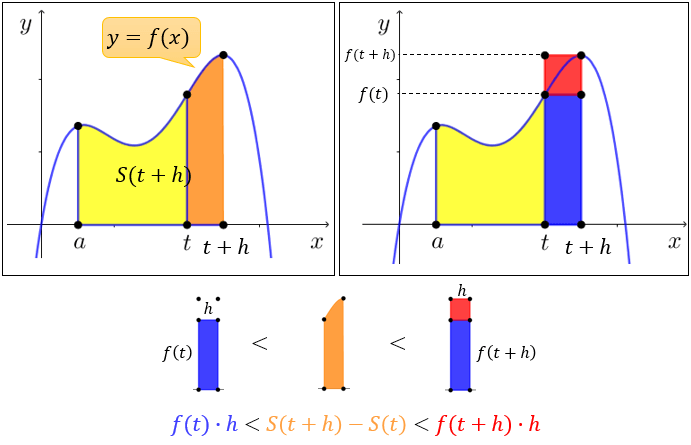
なぜ原始関数を使うのか,なぜ差なのか,そんなことをして何になるのか (教科書の項目として面積の項目は定積分の後に登場するが,)原始関数 F(x) は,関数 f(x) (>0) の下にできる図形の面積を表わし, F(b)−F(a) で a ≦ x ≦ b の区間の面積を表わせるので,このように定義すると豊かな応用そこで, 積分の値 ∫b a f(x)dx を考えるにあたっても,「長方形であれば, その面積につい てハッキリしたことが言える」ということに注目して, 以下で見るように,「短冊の面積の 極限値」として積分の値 ∫b a f(x)dx を定義するのが普通です 11 Riemann和面積 を求めよう。 面積は(上の関数)(下の関数)を から まで積分すれば良い。 この図では上の関数は 、下の関数は である。 したがって、面積は ここで、11での内容を思い出してほしい。
定積分によって面積を求める問題の解き方と公式
積分 面積 マイナス なぜ
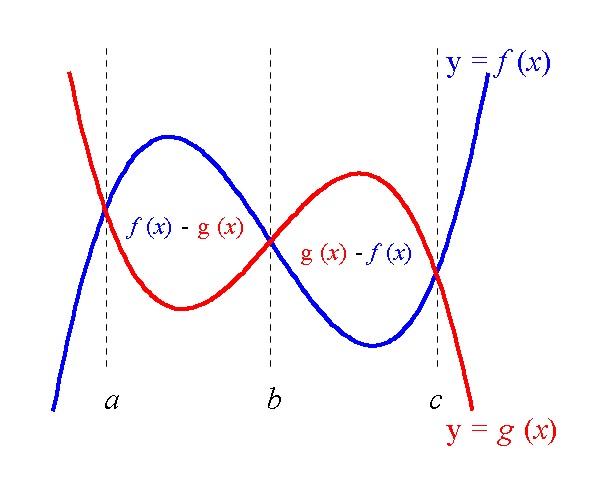
積分 面積 マイナス なぜ-微分の面積の問題でマイナスにするときとしないときの違いがわかりません!∫a,bf(x)dx = ∫b,af(x)dx って式がありましたよね。積分は、積分変数を走査する方向で正負が変わってしまいます。このため、積分で得られる「面積」は正負面積 を求めよう。 面積は(上の関数)(下の関数)を から まで積分すれば良い。 この図では上の関数は 、下の関数は である。 したがって、面積は ここで、11での内容を思い出してほしい。


積分してwi Fiをつなげよう 数学 統計教室の和から株式会社
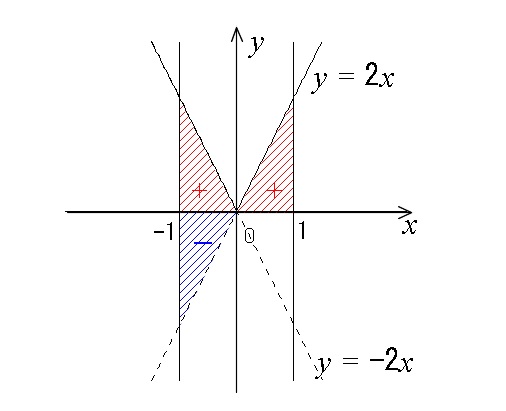
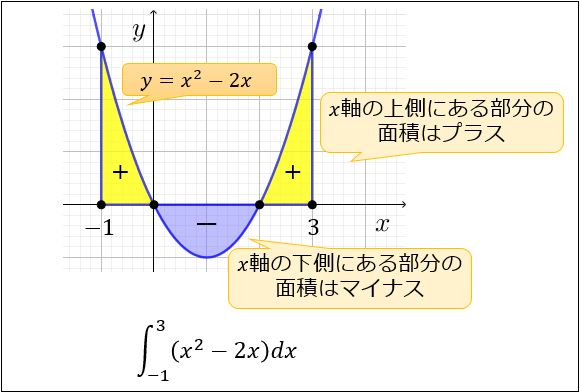
X軸の下側の部分の面積はマイナス ∫ − 1 3 (x 2 − 2 x) d x は、下図の 黄色い部分の面積 から 青い部分の面積 を 引いた値 を求めることを意味します。 実際に計算してみると、 ∫ − 1 3 (x 2 − 2 x) d x = 4 3 と求まります。頑張ってマイナスの面積を考えてみたいと思います。 例1) 曲線をa, bの範囲で積分したものは緑っぽい部分の面積から赤い部分の面積を引いたものになります。 曲線とt軸とで囲まれた面積を普通に考えるとプラスになりますが、図のように赤い部分の面積のほうが大きいと積分した値は円の面積の計算は,典型的な微積分の問題である.直観的に分かりやすいこの問題の解き方は,置換を使う積分 である: Integrate は, のような不適切な積分の多くに対して厳密解を返す:
また、マイナス3分のa>1というのもどこをどのように計算をして出たのか教えてください。 積分の応用なのですが、この問題だけわかりません。 よろしければ教えてください。 積分 面積 裏技公式 早見チャート「本当に,これで面積になっているの?」と言う方のために,右の図5で確かめてみて下さい。 図5では,関数 y=x 2 と2直線 x=0,x=3 と x 軸で囲まれた部分の面積 S を ・積分を用いる方法で求めた値 ・長方形で近似していく方法で求めた値(1) 積分で面積を求めるうえで,重要なのは関数の上下と 交点の 座標の 2 つです。 まずはグラフをかいて面積を求める図形と, 2 つの関数でどちらが上に位置するかを把握しましょう。 面積を求めるのは灰色の部分ということがわかります。ここでは が の 上に位置しているので,面積の公式
頑張ってマイナスの面積を考えてみたいと思います。 例1) 曲線をa, bの範囲で積分したものは緑っぽい部分の面積から赤い部分の面積を引いたものになります。 曲線とt軸とで囲まれた面積を普通に考えるとプラスになりますが、図のように赤い部分の面積のほうが大きいと積分した値は円の面積の計算は,典型的な微積分の問題である.直観的に分かりやすいこの問題の解き方は,置換を使う積分 である: Integrate は, のような不適切な積分の多くに対して厳密解を返す:面積がマイナス?色々な解釈で面積を正確に求める 積分で変な形の面積も求められるようになるとかなり自由に面積が求められるようになりそうなものですが、注意しなければいけないことがいくつかあります。 その1つが 求める面積の場所 です。


積分の問題でたまに面積がマイナスになる 18年03月01日のその他のボケ ボケて Bokete



X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫
面積分で出た値って負になることあるんですか?正になることも負になることもよくあります。面積分が実際の問題で出てくる場合、被積分関数はベクトル場であって、lim Σ F・ n ΔSのような形で登場するのが普通です。さらに、面には向きがよって、被積分関数を計算することができます。 最後に積分をしてフィナーレです。 この時、面積ベクトルが内向きであるため マイナスをつけます。 何とか求まりました! 1 面積ベクトルを求める 2 を で表す 3 を計算する の手順を踏めばよさそうです。さて、積分だ。 何をするかというと、面積を求めるわけだな。 この部分。 関数と軸の間の面積だ。もちろんxの値に依るのでF(x)とする。 でまあ、これを求める考え方としてはだな。 まず、細切れにする。 ここの幅はdxとする。微小な数だな。


自然科学のための数学14年度第12講



放物線と2直線で囲まれた面積s 高校数学に関する質問 勉強質問サイト
まあ面積を求める問題の解きは答えがマイナスになることは無いのでそこで気が付くと思います。 この公式の証明は積分を解いてみればすぐにできるので省略します。大切なのは、 左辺の式のカタチが図で見るとどんな意味を持つのか 、ということ。また、マイナス3分のa>1というのもどこをどのように計算をして出たのか教えてください。 積分の応用なのですが、この問題だけわかりません。 よろしければ教えてください。 積分 面積 裏技公式 早見チャート定積分がマイナスになるかどうか だけです。 ただの定積分を求めるために解く定積分の計算はマイナスになることがありますが、 面積を求めるために使う定積分では、マイナスになることはありません。 定積分$\,\displaystyle \int_{a}^{b}f(x)dx\,$の場合は、xで積分します。


定積分によって面積を求める問題の解き方と公式



X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫
微分の面積の問題でマイナスにするときとしないときの違いがわかりません!∫a,bf(x)dx = ∫b,af(x)dx って式がありましたよね。積分は、積分変数を走査する方向で正負が変わってしまいます。このため、積分で得られる「面積」は正負そこで, 積分の値 ∫b a f(x)dx を考えるにあたっても,「長方形であれば, その面積につい てハッキリしたことが言える」ということに注目して, 以下で見るように,「短冊の面積の 極限値」として積分の値 ∫b a f(x)dx を定義するのが普通です 11 Riemann和定積分と面積 定積分というわけのわからない計算を練習してきました。 ようやく定積分の実用を学習します。 定積分によって、曲線と \(x\) 軸とで囲まれた部分の面積が求まるのです。 定積分をすることで、なんとビックリ、面積が求まるのです・・・ なんだこれ?


積分



勉強しよう数学3c ループで囲まれた図形の面積の計算


積分とは何なのか 面積と積分計算の意味 アタリマエ



マーカーに引いたマイナスが付いている部分 高校数学に関する質問 勉強質問サイト



定積分によって面積を求める問題の解き方と公式


数学の図形の面積を求める問題で面積がマイナスになった 18年05月07日の人物のボケ ボケて Bokete



定積分 面積がマイナス Youtube
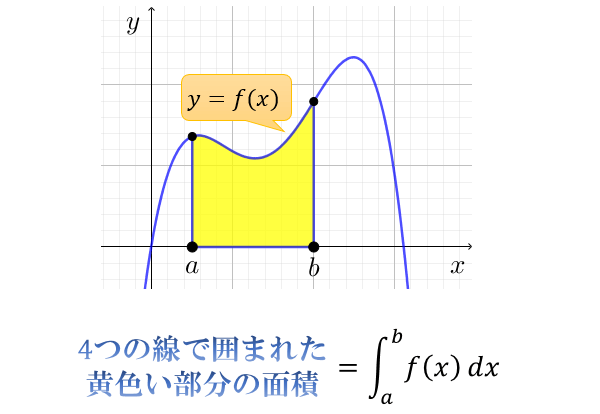


積分とは何なのか 面積と積分計算の意味 アタリマエ


定積分でx軸より下はなぜ面積なのにマイナスをつけるのですか 絶対値は Yahoo 知恵袋


積分とは何なのか 面積と積分計算の意味 アタリマエ
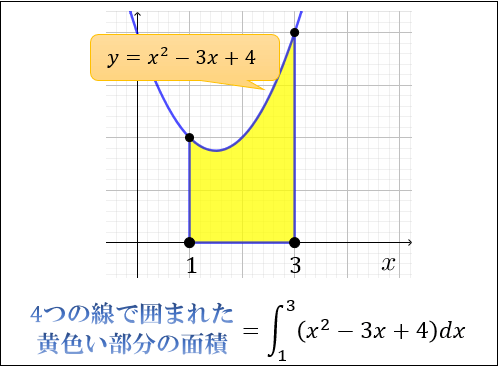


積分とは何なのか 面積と積分計算の意味 アタリマエ


数学の積分の問題がわからないので隣の奴の答案のぞいたら面積がマイナスになってた ナルトへのボケ ボケて Bokete



一夜漬け高校数学81 定積分 4つのパターン マイナスの面積 Youtube
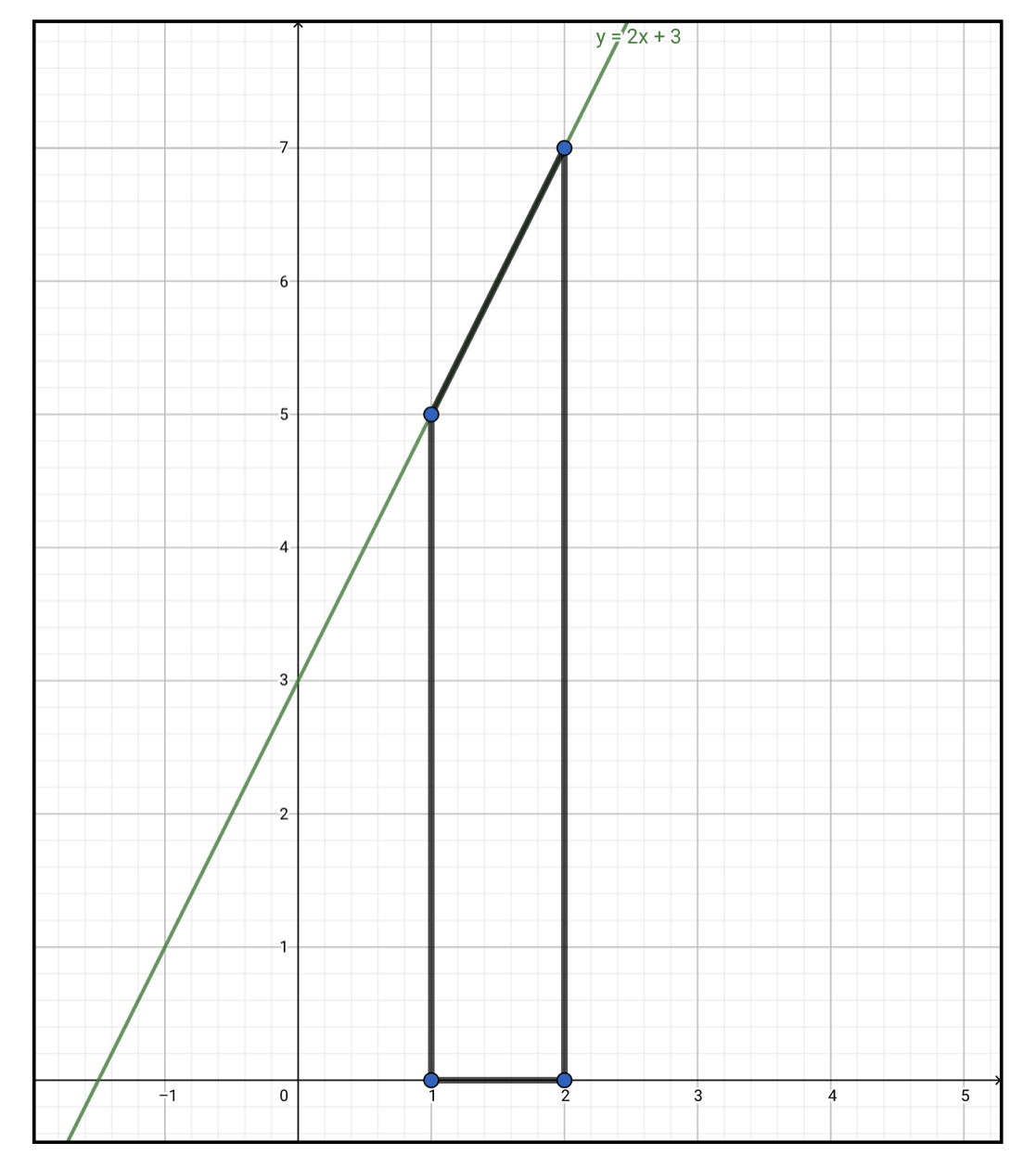


定積分のイメージ ぽこラボ勉強ブログ


何故面積はマイナスにならないのですか Quora


定積分の面積を求めるとき二乗とかの後にマイナスが付いてたら Yahoo 知恵袋



数2 定積分の範囲です ぐちゃぐちゃで申し訳ないのですが教えてください Clear



X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫



積分 面積 高校数学に関する質問 勉強質問サイト



基本 曲線とx軸の間の面積と積分 なかけんの数学ノート



数学ii 積分法 3 2 放物線とx軸で囲まれた部分の面積 Youtube



基本 曲線とx軸の間の面積と積分 なかけんの数学ノート
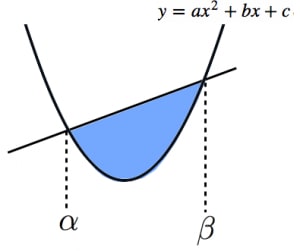


放物線と直線で囲まれた面積を高速で求める1 6公式 高校数学の美しい物語


数2の積分について 面積がx軸より下にできるとき 114のよう Yahoo 知恵袋



X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫



マイナス6分のの公式 定積分と面積 高校数学 Youtube



1 赤で丸印をつけた部分はなぜ 急にマイナスが出てくるのですか Clear


積分


積分の面積の問題についてです なぜ 2 0の範囲の面積は図 Yahoo 知恵袋



面積の計算について 数学 苦手解決q A 進研ゼミ高校講座 ベネッセコーポレーション



絶対値記号を含む定積分 数学 苦手解決q A 進研ゼミ高校講座 ベネッセコーポレーション



途中でマイナスを前に出して計算した結果答 高校数学に関する質問 勉強質問サイト



高校数学 B 積分 公式を使わずに面積を求める方法 やはり俺の考察ブログはまちがっている アニメ 数学



積分 面積 高校数学に関する質問 勉強質問サイト



こういう問題はどうしたら かっこの前にマイナスをつけることがわかるんですか 頂点がx Clear
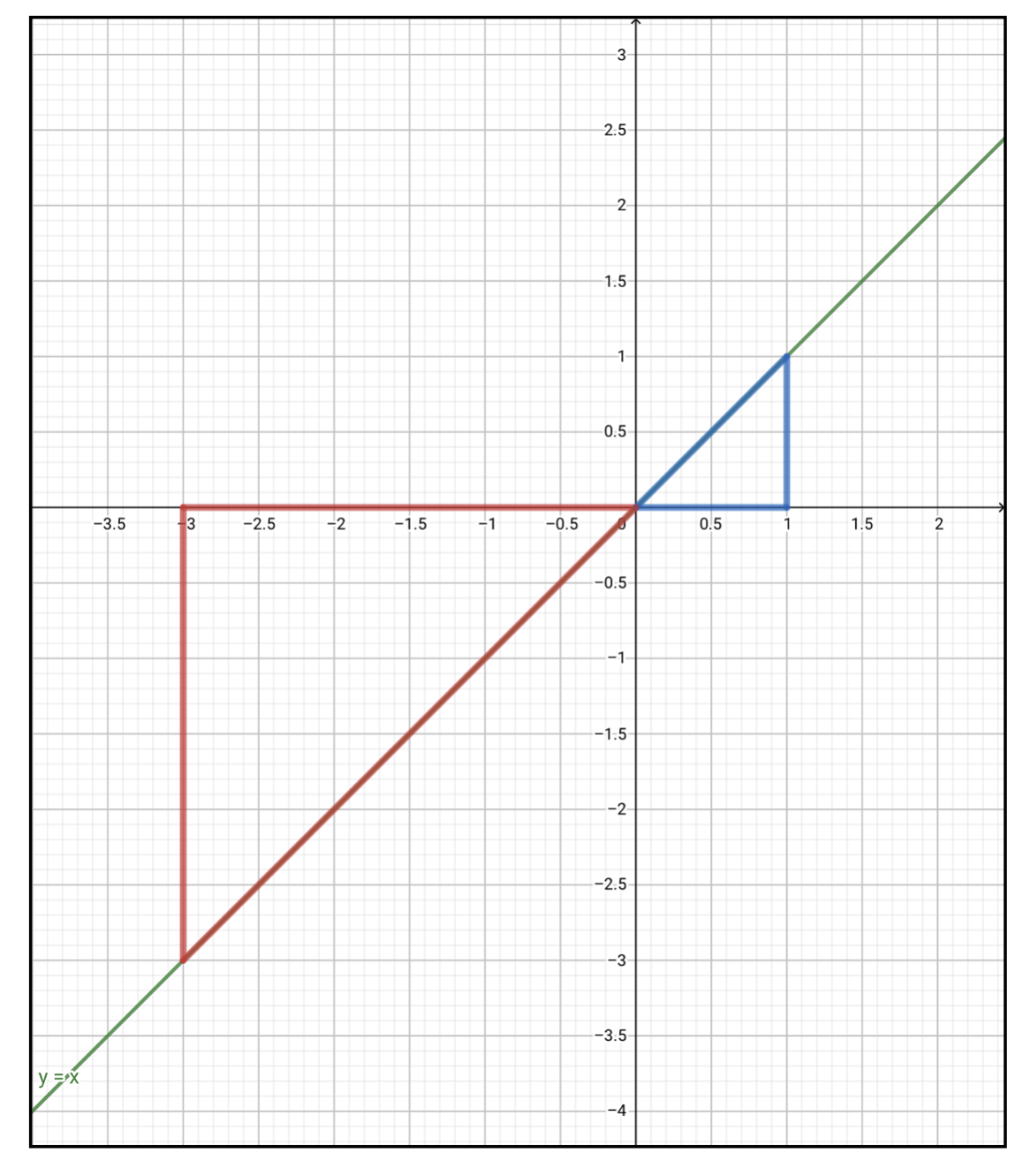


定積分のイメージ ぽこラボ勉強ブログ



楕円の知識まとめ 面積 方程式 焦点 接線 媒介変数表示 理系ラボ
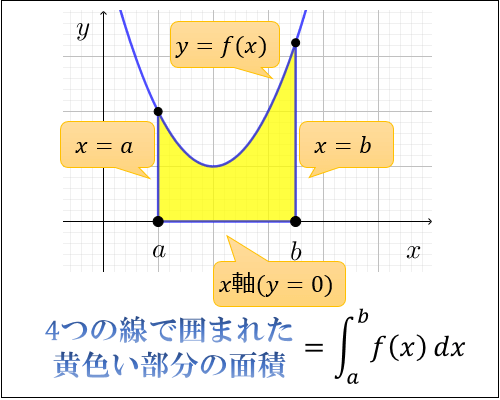


積分とは何なのか 面積と積分計算の意味 アタリマエ
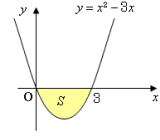


面積の計算について 数学 苦手解決q A 進研ゼミ高校講座 ベネッセコーポレーション


定積分と図形の面積の問題で 上 下をして面積を出すじゃないですか 青線 Yahoo 知恵袋


電気の基礎知識 数学の基礎知識 2 株式会社アイティ オフィス



微分 高階微分とマイナスの指数 大人が学び直す数学
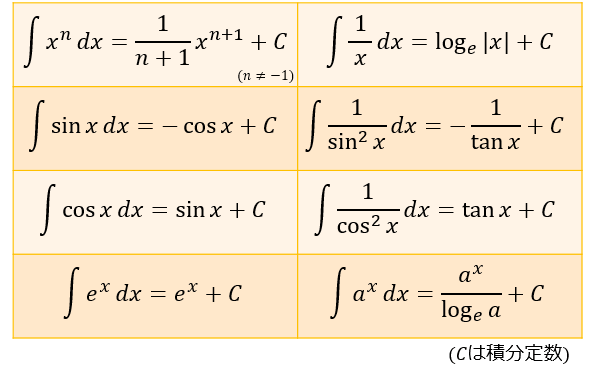


積分の公式一覧 アタリマエ
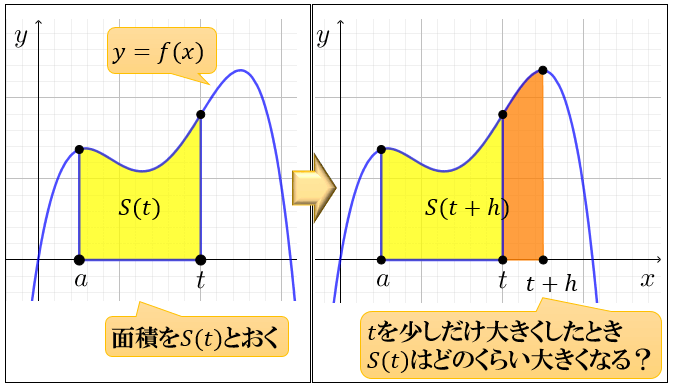


積分とは何なのか 面積と積分計算の意味 アタリマエ



高校数学 B 積分 公式を使わずに面積を求める方法 やはり俺の考察ブログはまちがっている アニメ 数学



符号付きの面積ってなに ー定積分で面積がマイナスになる理由 Youtube



数2 定積分の範囲です ぐちゃぐちゃで申し訳ないのですが教えてください Clear



途中でマイナスを前に出して計算した結果答 高校数学に関する質問 勉強質問サイト


Studydoctorマイナス6分のの公式 定積分と面積 高校数学 Studydoctor



1 の答えのところなんですけどなぜマイナスが付くのでしょうか X軸より下側にあるか Clear



積分してwi Fiをつなげよう 数学 統計教室の和から株式会社


積分の面積について のまえに をつける時ってどのような Yahoo 知恵袋


積分で図形の面積を求める問題で答えがマイナスになった 19年06月04日の人物のボケ ボケて Bokete



F X は関数を積分しているので 面積をあらわすと教わったのですが グラフではxが1 Clear



面積を積分して求めた時に答えがマイナスになってしまったら 面積がマイナスになる訳無 Clear


6分の1 12分の1 3分の1 A Day In Our Life



積分 2つの曲線の間の面積を求める公式の証明 数学ii By ふぇるまー マナペディア



X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫


数学の定積分と面積のところがわかりません画像のやつですマイナスがつく式ら Yahoo 知恵袋



符号付きの面積ってなに ー定積分で面積がマイナスになる理由 Youtube


数2で積分の面積をやってます 6 1公式で マイナスが付 Yahoo 知恵袋


積分の面積の問題です 丸く囲ったとこに 2とあるんですが なぜ Yahoo 知恵袋



積分で面積求めるときってy軸が負ならマイナスつけるのってひとつの線と軸の面積を求める Clear


数学で積分して面積を求める問題の答えがマイナスになった 年03月19日の人物のボケ ボケて Bokete



3分でわかる 定積分の性質 使い方のコツをわかりやすく 合格サプリ



図を書いてみて 面積がマイナスになってしまう所はマイナスをか 高校数学に関する質問 勉強質問サイト



勉強しよう数学 微分積分はどうすれば勉強できるか 2



面積の計算について 数学 苦手解決q A 進研ゼミ高校講座 ベネッセコーポレーション


高校数学について 積分における6分の1公式ってなぜマイナス6分の Yahoo 知恵袋


図形の面積を求める微分積分の問題で面積がマイナスになって焦る 19年01月09日のイラストのボケ ボケて Bokete
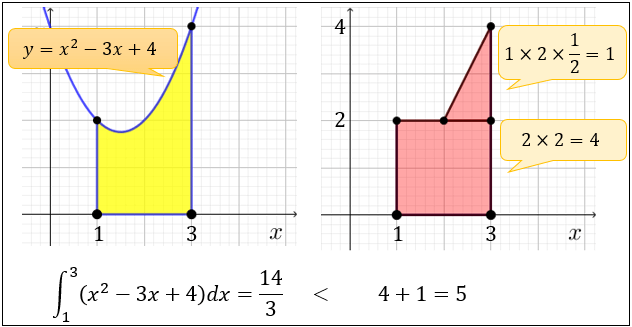


積分とは何なのか 面積と積分計算の意味 アタリマエ



平方完成とは一体何なのか なぜマイナスが出てくるのか 図形の面積 で解説 遊ぶ数学
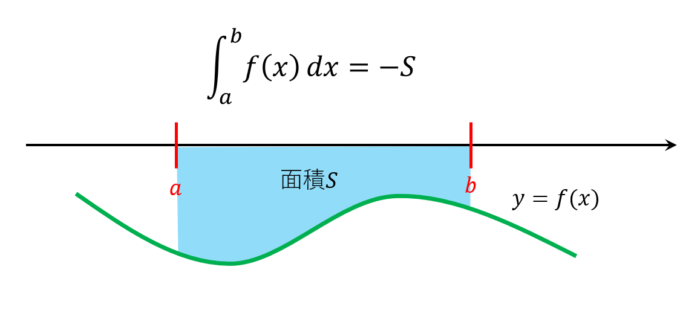


積分してwi Fiをつなげよう 数学 統計教室の和から株式会社



高校数学 B 積分 公式を使わずに面積を求める方法 やはり俺の考察ブログはまちがっている アニメ 数学
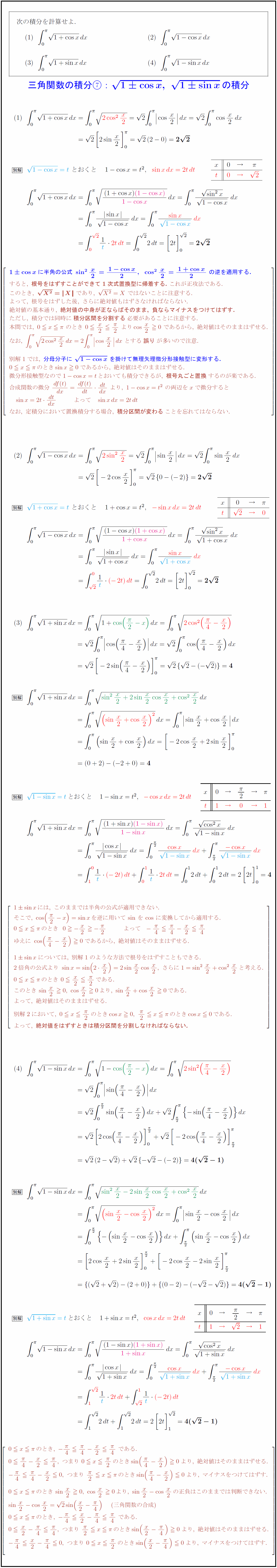


三角関数の積分 1 Cosx Dx 1 Sinx Dx 3つの解法 受験の月



X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫



なぜ定積分で面積が求まるのか 高校数学の美しい物語


積分の問題でなぜかマイナスになる面積 19年04月05日のその他のボケ ボケて Bokete


定積分でx軸より下はなぜ面積なのにマイナスをつけるのですか 絶対値は Yahoo 知恵袋


積分で面積を求める問題です 高校の授業で 面積が全部x軸より下にある場 Yahoo 知恵袋



交点を求めるとこまでは 分かります 面積を二等分する積分法の 高校数学に関する質問 勉強質問サイト


これは定積分の面積の問題で 放物線とx軸で囲まれた部分の面積 Yahoo 知恵袋


数学定積分で答えがマイナスになることがありますが なぜですか 定 Yahoo 知恵袋



標準 偶関数と奇関数の定積分 なかけんの数学ノート



この問題は何故かっこの前にマイナスがつくのですか Clear



数学 の定積分と面積の範囲 高校数学に関する質問 勉強質問サイト



なぜ定積分で面積が求まるのか 高校数学の美しい物語



この赤い線の部分の マイナスはなぜつくのでしょうか Clear



高校数学 X A M X B Ndxの計算技巧と1 6 1 12 1 30公式 受験の月



積分の面積公式を分かりやすく解説 まず理解して覚えよう 大学生の勉強部屋



面積を積分して求めた時に答えがマイナスになってしまったら 面積がマイナスになる訳無 Clear



面積を積分して求めた時に答えがマイナスになってしまったら 面積がマイナスになる訳無 Clear



0 件のコメント:
コメントを投稿